Super, ihr habt den Hinweis zur Öffnung des Ausgangs gefunden:



 ██████╗ 
██╔═══██╗
██║   ██║
██║   ██║
╚██████╔╝
 ╚═════╝ 


Dies ist der Hinweis damit ihr das Lösungswort-Anagram, also die drei Blöcke, übersetzen und korrekt anordnen könnt! Googelt einfach den folgenden Begriff: "l337 sp34k", um zu verstehen was die  Textzeichen bedeuten. Wenn ihr die Blöcke aus den drei Kompetenz-Checks richtig angeordnet habt, habt ihr das Lösungswort für den Ausgang aus dem Escape-Room! Ihr braucht das Lösungswort nicht zu übersetzen sondern sollte es in der l337sp34k Variante eingeben.

  _ ____ ____  _              ____  _  _   _   
 | |___ \___ \| |            |___ \| || | | |   
 | | __) |__) | |_   ___ _ __  __) | || |_| | __
 | ||__ <|__ <| __| / __| '_ \|__ <|__   _| |/ /
 | |___) |__) | |_  \__ \ |_) |__) |  | | |   < 
 |_|____/____/ \__| |___/ .__/____/   |_| |_|\_\
                        | |                     
                        |_|
BWL-Check
Ute Lübke

Elementare Funktionslehre

Aufgabe:

Welche Funktionsvorschrift liegt dem abgebildeten Graphen zugrunde?

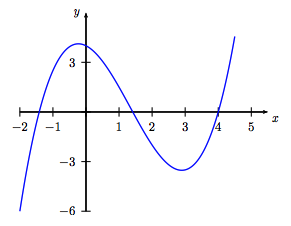
Graphen

Antwortmöglichkeiten:

a) $f_1(x)=-e^{x}\quad(x\in\mathbb{R})$

b) $f_2(x)=\frac{1}{2}x^3-2x^2-x+4\quad(x\in\mathbb{R})$

c) $f_3(x)=\frac{1}{x+4}\quad(x\in\mathbb{R}\backslash\{-4\})$

d) $f_4(x)=-\sqrt{x^2+4x}\quad(x\in\mathbb{R}_+)$

Hinweise zur Aufgabe:

Führen Sie sich den üblichen Verlauf der angegebenen Funktionstypen

a) Exponentialfunktion
b) Polynomfunktion
c) gebrochen-rationale Funktion (Hyperbel)
d) Wurzelfunktion

vor Augen und ordnen Sie so den Graphen der Funktionsvorschrift zu. Beachten Sie bspw. auch den $y$-Achsenabschnitt der abgebildeten Funktion.

Lösung: b)

Ausführliche Lösung:

Bei dem abgebildeten Funktionsgraphen handelt es sich um eine Polynomfunktion dritten Grades, da sie den für Polynome dritten Grades typischen $S$-förmigen Verlauf besitzt. Zudem weist der Graph seinen $y$-Achsenabschnitt bei $y = 4$ auf – auch dies ist konsistent mit $f_2(0) = 4$.

Hinweise zur Lösung:

Die Funktionsverläufe aller angegebenen Funktionen sehen wie folgt aus:

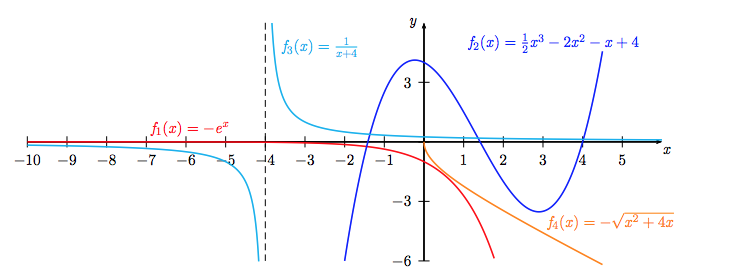
Funktionsverlauf

$f_1(x)$: Exponentialfunktionen verlaufen typischerweise streng monoton steigend und streng konvex. Da die in a) angegebene Exponentialfunktion ein negatives Vorzeichen besitzt, kehren sich die Eigenschaften in ihr Gegenteil, weshalb $f_1(x)$ streng monoton fallend und streng konkav verläuft (das negative Vorzeichen bewirkt eine Spiegelung über die $x$-Achse).

$f_3(x)$: Gebrochen-rationale Funktionen vom Typ $f(x)=\frac{ a }{ x+b }+c$ sind Hyperbeln und besitzen typischerweise an der Stelle ihrer Definitionslücke (hier: $x = -4$) eine vertikale Asymptote (gestrichelte Linie). Bei dieser Definitionslücke handelt es sich genauer um eine sog. Polstelle, da der Funktionsgraph in der Nähe von $x = -4$ jeweils divergiert, d.h. gegen $\pm\infty$ läuft.

$f_4(x)$: Typischerweise verlaufen Wurzelfunktionen streng monoton steigend und streng konkav. Da die in d) angegebene Wurzelfunktion ein negatives Vorzeichen besitzt, kehren sich die Eigenschaften in ihr Gegenteil, weshalb $f_4(x)$ streng monoton fallend und streng konvex verläuft.